На главную Теория Задачи Учёные Интересные статьи Шкала скоростей Карта сайта

Kинематика равномерного вращения по окружности

При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение

a_ц = v²/R,

где R - радиус окружности.

Вывод формулы для центростремительного ускорения

По определению

На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что |r1| = |r2| = R и |v1| = |v2| = v, из подобия треугольников находим:

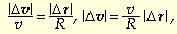
откуда

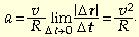
Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j₀), y = R sin(j + j₀),

где j₀ определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).

В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:

j = wt,

где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c^-1 = Гц.

Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.

Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:

x = R cos(wt + j₀),
y = R sin(wt + j₀).

Время, за которое совершается один оборот, называется периодом T.

Частота

n = 1/T.

Размерность частоты: [n] = с^-1 = Гц.

Связь циклической частоты с периодом и частотой: 2p = wT, откуда

w = 2p/T = 2pn.

Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда

v = 2pR/T = wR.

Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:

a_ц = v2/R = w2R = 4p2n2R = 4p2R/T2.

Связь поступательного и вращательного движений

Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:

перемещение s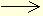угловое перемещение j = s/R;
скорость v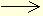угловая скорость w = v/R;
ускорение a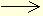угловое ускорение a = a/R.

Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:

s = vt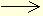j = wt,
v = v₀ + at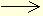w = w₀ + at.

Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:

v = wR.

Задачи на эту тему