На главную Теория Задачи Учёные Интересные статьи Шкала скоростей Карта сайта

Основные понятия механики

      

Изменение положения тела в пространстве по отношению к другим телам с течением времени называется механическим движением. Раздел физики, изучающий механическое движение, называется механикой. Раздел механики, изучающий движение тел независимо от причин, вызвавших это движение, называется кинематикой.       

При движении в пространстве точки тела описывают траектории.       

Простейшими видами механического движения являются поступательное движение (такое движение, при котором прямая, проведенная через любые две точки тела, перемещается параллельно самой себе) и вращательное движение (все точки тела описывают концентрические окружности вокруг общей оси).      

Во многих случаях движущееся тело можно рассматривать как материальную точку (если размеры тела малы по сравнению с расстояниями до других тел). Если это не оговорено особо, во всех задачах механики, рассматриваемых ниже, это условие выполняется, так что можно говорить о движении материальных точек. Например, расстояние от Земли до Солнца (1,5·108 км) много больше размеров как Земли (6,4·103 км), так и Солнца (7·105 км), поэтому с хорошей точностью можно рассматривать движение этих (и всех других) тел Солнечной системы как движение материальных точек. При изучении полета теннисного мяча можно во многих случаях пренебречь его размерами. Тем более это справедливо при изучении движения пучка заряженных элементарных частиц в магнитном поле.       

Движение тела в пространстве математически описывается в произвольно выбранной системе отсчета. Система отсчета состоит из:

1. Тела отсчета О.
2. Системы координат (в данном случае декартовой).
3. Часов, синхронно идущих во всех точках пространства.

      

С точки зрения наблюдателей в разных системах отсчета одно и то же движение может выглядеть совершенно по-разному. Механическое движение относительно.       

Положение материальной точки в пространстве в заданный момент времени определяется радиусом-вектором этой точки r(t). В декартовой системе координат
      

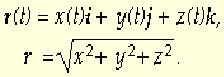
Задание декартовых компонент x(t), y(t) и z(t) как функций времени определяет закон движения материальной точки. Частными случаями движения являются движение в заданной плоскости (для его описания достаточно двух координат x(t) и y(t)) и движение вдоль заданной прямой (ее всегда можно выбрать за ось x декартовой системы).       

При движении материальной точки конец радиуса-вектора, проведенного в эту точку, описывает траекторию. Каждая точка траектории соответствует значениям координат x, y, z в данный момент времени. Например, при движении на плоскости траектория может быть задана как кривая, описываемая функцией y(x). Длина траектории между начальной и конечной точками называется путем, а вектор, соединяющий начальную и конечную точки пути, называется перемещением. Если начальная и конечная точки заданы радиусами-векторами r₁ и r₂, то перемещение s = r₂ – r₁.       

Напомним, что векторы складываются по правилу параллелограмма одним из двух эквивалентных способов:       

а) начала двух векторов совмещаются, и на этих векторах строится параллелограмм, диагональ которого равна сумме векторов;

      

б) начало второго вектора совмещается путем параллельного переноса с концом первого вектора, и проводится вектор, соединяющий начало первого и конец второго векторов.

      

Если точка последовательно совершает несколько перемещений, то полное перемещение равно векторной сумме отдельных перемещений:       

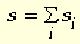
Следует обратить внимание на то, что величина перемещения s = |s|, вообще говоря, не совпадает с путем (например, вернувшись в ту точку, откуда начато движение, тело проходит отличный от нуля путь, но перемещение равно нулю). В случае одномерного движения перемещение s = x – x₀ может быть как положительным, так и отрицательным.      

 Единицами измерения пройденного пути и времени в СИ являются метр (м) и секунда (с). Размерность какой-то физической величины обозначается символом этой величины в квадратных скобках. Таким образом, [l] = м, [t] = с.

Задачи на эту тему