На главную Теория Задачи Учёные Интересные статьи Шкала скоростей Карта сайта

Кинематика равномерногo поступательного движения

Средняя скорость движения материальной точки за интервал времени 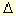t = t₂ - t₁ определяется как

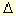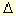Здесь r = s - перемещение тела за время t.

Размерность скорости: [v] = м/с.

Если движение таково, что средняя скорость за любой промежуток времени не меняется ни по величине, ни по направлению, то такое движение называется равномерным прямолинейным движением. В этом случае

s = vt,

где v = const и отсчет времени начат от момента t₁ = 0, так что можно принять 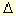t = t. В случае равномерного прямолинейного движения путь совпадает с модулем перемещения.

Формула для перемещения при равномерном движении есть первый пример математической записи определенного физического закона. Этот закон имеет вид равенства одного вектора (s) другому вектору (vt). Следует всегда помнить, что это сокращенная форма записи трех равенств:
s_x = v_xt, s_y = v_yt, s_z = v_zt
в произвольно выбранной декартовой системе координат. Другой тип математической записи физических законов, встречающийся в школьном курсе физики, - равенство одного числа (или скаляра) другому числу: А = В.

Уравнения прямолинейного равномерного движения принимают наиболее простой вид в системе координат, одна из осей которой (например, ось x) направлена вдоль вектора скорости v. Тогда компоненты скорости будут: v_x = v, v_y = 0, v_z = 0. Уравнения прямолинейного равномерного движения вдоль оси x:

s_x = vt или x - x₀ = vt.

Преобразования Галилея

Всякое событие характеризуется местом, в котором оно произошло, и моментом времени, когда оно произошло, измеренными в определенной системе отсчета. Иными словами, событие характеризуется четырьмя координатами (x, y, z; t).

Если одна система отсчета движется относительно другой равномерно и прямолинейно со скоростью V (для определенности, эта скорость направлена вдоль оси x), то координаты одного и того же события в этих системах связаны соотношениями:

t =t',
x =x' + Vt',
y =y',
z =z'.

В векторной форме записи:
t = t', r = r' + Vt'.

Здесь r и r' - радиусы-векторы произвольной точки Р в двух системах отсчета. Отметим, что в этих формулах предполагается (постулируется), что время события одинаково в любой системе отсчета, равномерно движущейся относительно данной системы (подробнее см. теория относительности).

Если принять, что точка Р движется равномерно и прямолинейно, то r = r₀ + vt, r' = r₀' + v't, где v и v' - скорости точки в двух системах отсчета. Если отсюда найти перемещения 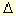r = vt и 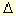r' = v't, подставить их в формулу преобразования Галилея и поделить на t, получится закон сложения скоростей в классической механике:

v = v' + V.

Этот закон, конечно, верен не только для равномерного, но и для произвольного движения. Таким образом, скорость тела v относительно (условно) неподвижной системы отсчета 1 равна векторной сумме скорости тела v' относительно движущейся системы отсчета 2 и скорости движения V самой системы 2 относительно системы 1.

Задачи на эту тему